Chaotic Attractors
A downloadable game
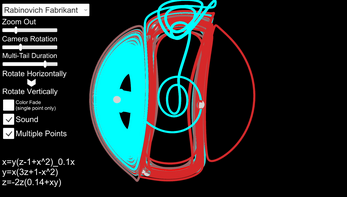
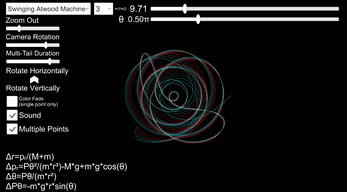
This application provides a simulation of over two dozen variations of chaotic attractors. I looked through many research papers and online articles, tinkered with the equations that resulted in some of the most visually interesting outputs, and collected them all in one place. I find it very soothing to have this simulation up on an extra monitor similar to a screensaver. It also has a Swinging Atwood's Machine where you can vary the starting conditions to see how the system evolves over time.
A chaotic attractor is a series of equations that cause a point to evolve over time in a such a way that it eventually passes through all points within an attraction region. In other words, if you take any two points selected randomly that are within the possible outputs of the attractor, those two points will eventually become arbitrarily close to each other.
One of the first practical examples of these equations was when scientists were trying to predict the weather. They noticed that with simple deterministic equations, modifying the inputs by miniscule amounts resulted in drastically different weather patterns. This kicked off the field of chaos theory.
| Status | Released |
| Author | BenderiteGames |
| Genre | Simulation, Educational |
| Tags | chaos, Math |
Download
Click download now to get access to the following files:

Leave a comment
Log in with itch.io to leave a comment.